The Acquasanta Railway Viaduct

Mazzieri I., M.Stupazzini, R.Guidotti, C.Smerzini: SPEED: SPectral Elements in Elastodynamics with Discontinuous Galerkin: a non-conforming approach for 3D multi-scale problems, Int. J. Numer. Meth. Eng., (2013); 12: 991-1010.

Introduction

On the Genoa-Ovada railway, NW Italy, km 18+519.35, is located the Acquasanta bridge, in the Genoa district. The bridge represents a typical structure the ancestor of which can be dated back to the Roman Age and, thanks to the excellent design achieved no less than two thousand years ago, this structural type did not change significantly along the centuries. The Acquasanta bridge structure  is remarkable, both for the site features and the local geological and geomorphological conditions. The foundations of several of the piers, indeed, rest on weak rock; moreover, some instability problems have been detected in the past on the valley slope towards Ovada (west side), although no warnings have been recently reported.

Acquasanta railway bridge on the Genoa-Ovada railway.

Acquasanta railway bridge on the Genoa-Ovada railway.

Progressive zoom of 3D models of Acquasanta bridge and the surrounding geological configuration.

Progressive zoom of 3D models of Acquasanta bridge and the surrounding geological configuration. Left: Conforming mesh in which different colors identify materials with different mechanical properties; Right: non-conforming mesh, in which different colors identify different sub-domains, independently meshed and then combined.

3D model of the Acquasanta bridge

The considered problem, including both the structure and its surrounding area, involves very different spatial scales, from that of the geological model (hundreds of meters) to that of the bridge details (tens of centimeters). Two different meshes were constructed, one relying on a classical conforming spectral element approach, and another one by using the Discontinuous Galerkin approach implemented in SPEED. In particular, the need to accomplish the complex geometry of the Acquasanta viaduct and of the surrounding alluvial deposits as well implied, in the conforming approach, the adoption of a huge number of deformed elements up to the bottom of the model. Using a standard conforming mesh, indeed, such a multi-scale description can be obtained only through subsequent refinements, yielding a significant increase of the number of elements, a worsening of their quality and therefore the growth of the computational burden of the problem.

Mechanical characteristics of the different materials.

Mechanical characteristics of the different materials.

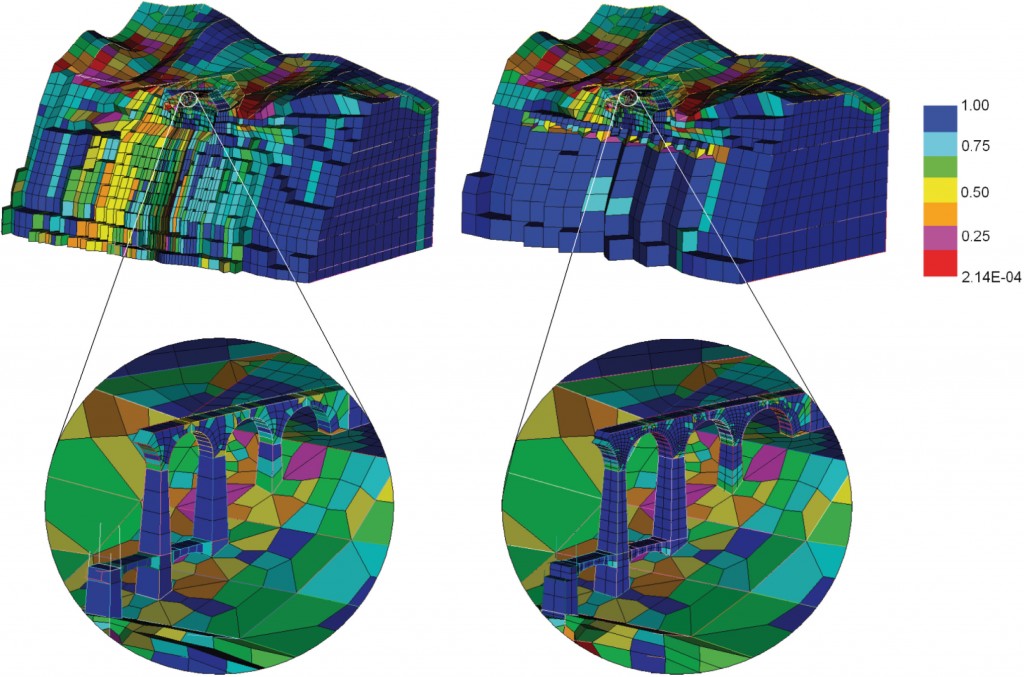
Quality metrics, here represented as a function of the Jacobian of the element.

Quality metrics, here represented as a function of the Jacobian of the element.

Quality of the computational mesh

Transversal section of the two 3D models with zoom on the Acquasanta bridge. The non-conforming mesh (right) is characterized by a lower number of hexahedra (20.602 with respect to 38.569 elements), and by a better level of quality metrics, here represented as a function of the Jacobian of the element ( almost 50% of elements with excellent quality-blue color). More elements where it is necessary for a proper description (bridge) and less elements where it is not (deep rock).

 

Numerical Results

An excellent agreement is found between the confirming and the non-conforming approach. Some representative results of the numerical simulation are reported in terms of snapshots of the displacement of the Acquasanta bridge. It is possible to observe, through the  snapshots, the movement of the deck and piers of the bridge.

Snapshots (t = 0.3, 0.6 and 0.9 s, from left to right) of the simulated displacement of the Acquasanta viaduct.

Snapshots (t = 0.3, 0.6 and 0.9 s, from left to right) of the simulated displacement of the Acquasanta viaduct. Displacements are considered in their absolute values. An amplification factor has been adopted for visualization purpose.