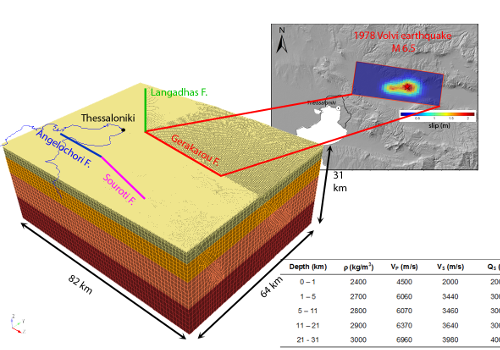
Geological dataset
Thessaloniki, the second largest city in Greece, is located in the Axios-Vardar zone, which is adjacent to the Servomacedonian massif, extending from the Yugoslavia-Bulgaria border up to the North Aegean Trough. The Servomacedonian massif is one of the most seismotectonically active zone in Europe; a large portion of its seismicity is associated to the Mygdonia graben, around 25 km northeast of Thessaloniki, where on 20 June 1978 a destructive earthquake with moment magnitude MW ≥ 6.5 occurred.
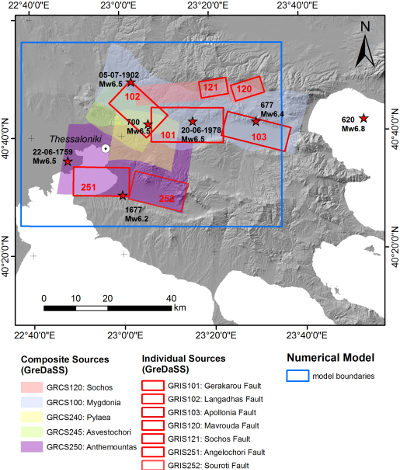
Digital Elevation Model (DEM) of the broader area under study with indication of the main seismic sources of interest (from GreDASS database: GRCS = GReek Composite Source; GRIS = Greek Individual Sources, i.e. faults) and the epicenters (denoted by the stars) of most destructive historical earthquakes with Mw ≥ 6. The boundaries of the SPEED model are also superimposed (blue box).
3D spectral element mesh for the broader Thessaloniki area. The crustal model, the faults included in the model and the slip distribution for the 1978 Volvi earthquake are also shown.
Numerical Model
Based on the available data regarding both the characterization of the seismic sources and geological, geotechnical and geophysical aspects, a large-scale 3D spectral element model has been constructed, including the following features, as key ingredients:
- ground topography as retrieved from 90 m SRTM DEM (http://srtm.csi.cgiar.org/);
- four seismogenic fault sources posing a hazard to the city of Thessaloniki, specifically, Gerakarou– GRIS101 (i.e., the fault responsible of the 1978 Volvi earthquake), Langadhas-GRIS102, Angelochori-GRIS251, and Souroti-GRIS252 (the latter two being part of the Anthemountas fault zone);
- horizontally layered crustal model for deep rock materials (from Ameri et al., 2008);
- 3D subsoil model of the Thessaloniki urban area, based on the detailed microzonation geotechnical studies (Anastasiadis et al., 2001) combined with extensive geophysical analyses (Apostolidis et al., 2004).
This model can propagate frequencies up to about 2 Hz.
Numerical Results
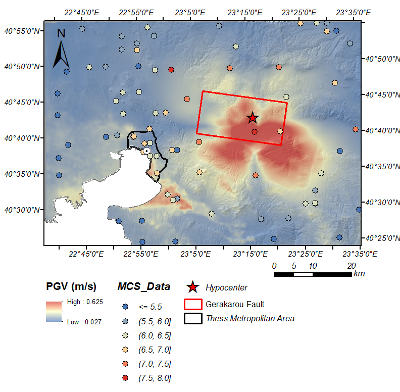
Peak Ground Velocity Map
The deterministic simulations reproduce the spatial variability of ground motion up to 2.0 Hz reasonably well, as highlighted by the good agreement between the simulated PGV (Peak Ground Velocity) and the distribution of regional spatial distribution of the MCS intensities measured during post-earthquake surveys.
Spatial variability of PGV (geometric mean of horizontal components) compared with the regional distribution of MCS intensity during the 1978 Volvi earthquake.
Comparison with recorded ground motions
The comparison between synthetics and ground motion observations at the accelerometric station THE-City Hotel in terms of velocity waveforms and Fourier amplitude spectral demonstrates satisfactory agreement especially for the horizontal components.
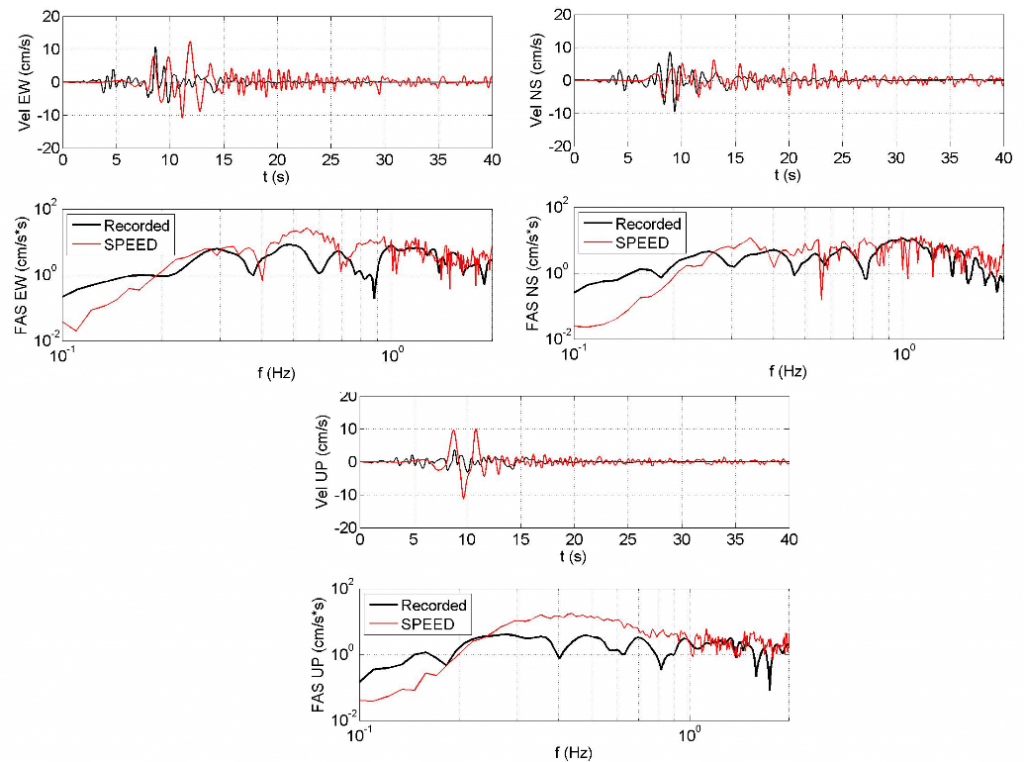
Comparison between synthetics and recordings at the THE-City Hotel station in terms of three component velocity time histories and corresponding Fourier amplitude spectra (FAS). Data are filtered in the range 0.25-2 Hz.
Comparison with ground motion prediction equations (GMPEs)
The numerical simulation results can also be utilized for investigating the accuracy of available empirical equations in prediction of ground motion in Thessaloniki metropolitan area. The comparison is presented with the GMPE proposed by Akkar et al. (2014) based on earthquake records in Europe and the Middle East as well as the empirical peak ground motion predictive relations from Skarlatoudis et al. (2004) for shallow earthquakes in Greece and the broader Aegean area.
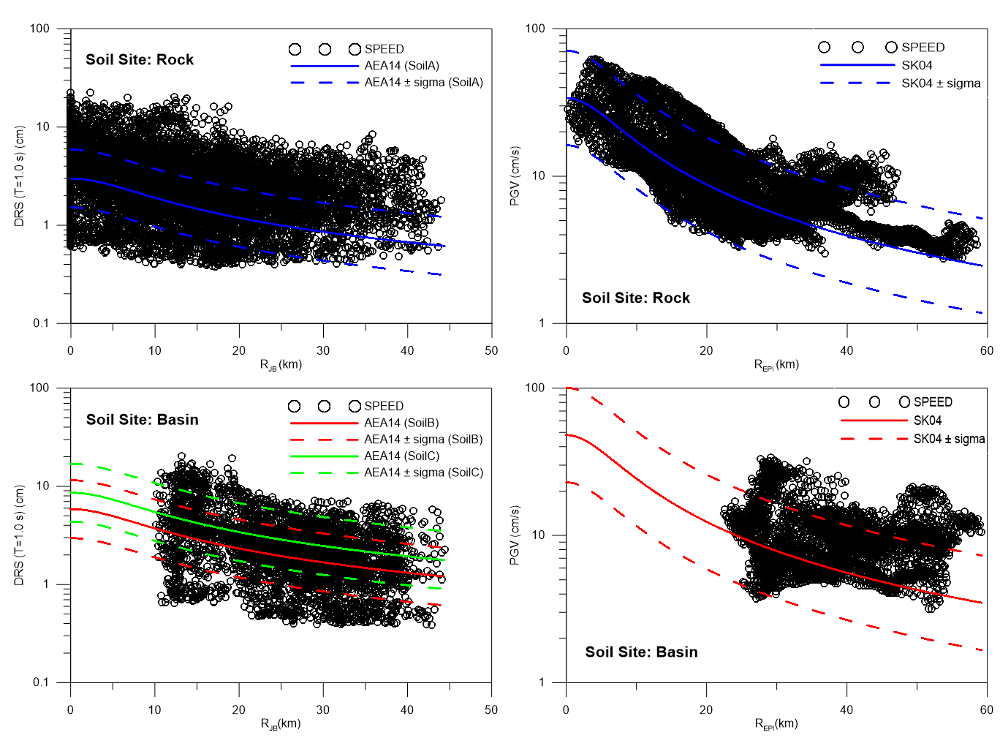
Left: Comparison of simulated PGV (geometric means of horizontal components) values by SPEED and the empirical prediction proposed by Skarlatoudis et al. 2003 with respect to epicentral distance metric Repi at receivers on the rock (top) and alluvial basin (bottom). Right: Comparison between numerical simulation by SPEED and GMP equation proposed by Akkar et al. 2014 in terms of Displacement Response Spectra (DRS) at period T=10 s of with respect to Joyner-Boore distance metric Rjb at receivers on the rock (top) and alluvial basin (bottom).
References
Ameri, G., Pacor, F., Cultrera, G. and Franceschina, G., 2008. Deterministic ground-motion scenarios for engineering applications: the case of Thessaloniki, Greece, Bull. seism. Soc. Am., 98(3), 1289-1303.
Anastasiadis, A., Raptakis, D. and Pitilakis, K., 2001. Thessaloniki’s detailed microzoning: subsurface structure as basis for site response analysis, Pure appl. Geophys., 158, 2597-2633
Apostolidis, P., Raptakis, D., Roumelioti, Z. and Pitilakis, K., 2004. Determination of S-wave velocity structure using microtremors and SPAC method applied in Thessaloniki (Greece), Soil Dyn. Earthq. Eng., 24, 49-67.
Akkar, S., Sandıkkaya, M. A., Bommer, J. J., 2014. Empirical ground-motion models for point- and extended-source crustal earthquake scenarios in Europe and the Middle East. Bull. Earthquake Engineering, 12, 359–387, doi: 10.1007/s10518-013-9461-4
Skarlatoudis, A. A., Papazachos, C. B., Margaris, B. N., Theodoulidis, N., Papaioannou, Ch., Kalogeras, I., Scordilis, E.M, Karakostas, V., 2003. Empirical Peak Ground-Motion Predictive Relations for Shallow Earthquakes in Greece. Bull. seism. Soc. Am., 93(6), 2591–2603