MAKE_LGL_NW.f90 File Reference

Go to the source code of this file.

Functions/Subroutines
subroutine	make_lgl_nw (nb_pnt, xq, wq, dd)
	Makes Gauss-Legendre-Lobatto nodes, weigths and spectral derivatives.

Function/Subroutine Documentation

make_lgl_nw()

subroutine make_lgl_nw	(	integer*4, intent(inout)	nb_pnt,
		real*8, dimension(nb_pnt)	xq,
		real*8, dimension(nb_pnt)	wq,
		real*8, dimension(nb_pnt,nb_pnt)	dd
	)

Makes Gauss-Legendre-Lobatto nodes, weigths and spectral derivatives.

Author

Ilario Mazzieri

Date

September, 2013

Version

1.0

Parameters

[in]	nb_pnt	polynomial degree
[out]	xq	LGL nodes
[out]	wq	LGL weights
[out]	dd	matrix for spectral derivatives

Definition at line 28 of file MAKE_LGL_NW.f90.

      
     implicit real*8 (a-h,o-z)
      
      parameter(nstep = 1000, acc = 1.d-15)
      
      
      integer*4, intent(inout) :: nb_pnt
      real*8, dimension(nb_pnt) :: xq, wq      
      real*8, dimension(nb_pnt) :: dd(nb_pnt,nb_pnt)
              
      n = nb_pnt-1
      xq(1) = -1.d0
      xq(nb_pnt) = 1.d0
      n2=idint(0.5d0*nb_pnt)
      dx=2.d0/dfloat(nstep)
 
      x = -1.d0
      iroot = 1
 
      call get_legendre_value(p2,a1,p1,p1der,n,x)
      
      do while (iroot .lt. n2)
        x = x + dx
        call get_legendre_value(p2,a2,p1,p1der,n,x)
        
        if (dabs(a2) .le. acc) then
          iroot = iroot + 1
          xq(iroot) = a2
        else
          aa = a1 * a2
          if (aa .lt. 0.d0) then
            iroot = iroot + 1
            xq(iroot) = find_root_pol(x-dx,x,acc,n)
          endif
        endif
        
        a1 = a2
      enddo
      
      n_filt = 2*n2
      if (n_filt .ne. nb_pnt) then         ! nb_pnt odd
        xq(n2+1) = 0.d0
        do i = 1, n2-1
          xq(nb_pnt-i) = -xq(i+1)
        enddo
      else                           ! nb_pnt even
        do i = 1, n2-1
          xq(nb_pnt-i) = -xq(i+1)
        enddo
      endif
      
      
      xn = dfloat(n)
      acost = 2.d0/(xn*(xn+1.d0))
      
      do j = 1,nb_pnt
         call get_legendre_value(p2,p2der,p1,p1der,n,xq(j))
         den = p2*p2
         wq(j) = acost/den
         
         do i = 1, nb_pnt
            if (i .ne. j) then
               call get_legendre_value(pnum,p2der,p1,p1der,n,xq(i))
               den = p2 * (xq(i)-xq(j))
               dd(i,j) = pnum / den
            endif
         enddo
         
      enddo
      
      do j = 2, nb_pnt-1
         dd(j,j) = 0.d0
      enddo
      
      dd(1,1) = -0.25d0 * xn * (xn+1.d0)
      dd(nb_pnt,nb_pnt) = 0.25d0 * xn * (xn+1.d0)
     
      
      return
      

References find_root_pol(), and get_legendre_value().

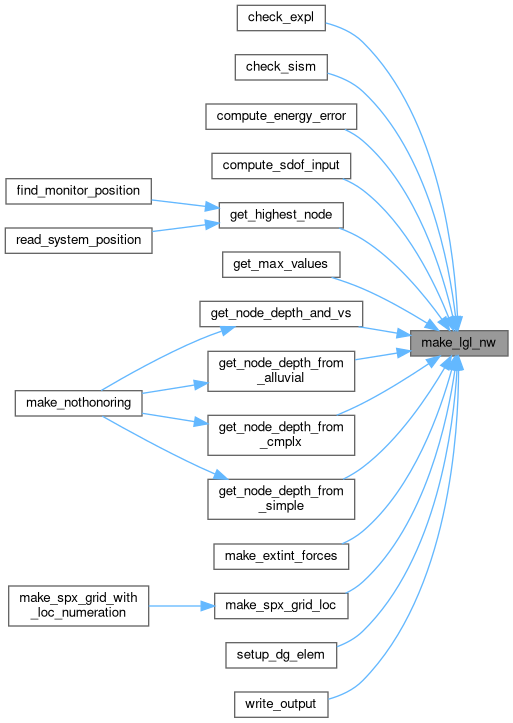
Referenced by check_expl(), check_sism(), compute_energy_error(), compute_sdof_input(), get_highest_node(), get_max_values(), get_node_depth_and_vs(), get_node_depth_from_alluvial(), get_node_depth_from_cmplx(), get_node_depth_from_simple(), make_extint_forces(), make_spx_grid_loc(), setup_dg_elem(), and write_output().

Here is the call graph for this function:

Here is the caller graph for this function: